티스토리 뷰
오늘의 1원은 내일의 1원보다 가치 있다
1999-10-18
화폐의 시간가치(Time value of money)
화폐의 가치는 시간에 따라 달라집니다. 동일한 화폐가 왜 시간에 따라 다른 가치를 갖게 될까요? 어떤 사람에게 "오늘 1000만 원을 줄까, 내년에 1000만 원을 줄까?"라고 질문을 하면 모두 오늘 1000만 원을 택하려 할 것입니다. 오늘 1000만 원이 내년 1000만 원보다 더 화폐가치가 높다고 생각합니다. 왜 그것이 합리적인지 생각해 봅시다.

첫 번째 이유는 인플레이션입니다. 자본주의 경제는 거의 필연적으로 인플레이션이 나타납니다. 경제가 성장함에 따라 물가가 오르기 때문에 시간이 흐를수록 화폐가치가 상대적으로 더 떨어지는 경우가 많습니다.
그 다음으로, 자본주의 사회에는 생산 기회(production opportunity)가 있기 때문입니다. 오늘 1000만 원을 받아서 다른 이윤을 남겨줄 수 있는 투자처에 투자할 수 있습니다. 내년 1000만 원을 택한다는 것은 투자할 기회를 포기한다는 측면에서 합리적이지 않습니다.
그리고 화폐의 시차 선호(time preference) 경향이 현재쪽으로 치우쳐 있기 때문입니다. 대부분의 사람들은 다른 차이가 없다면 내일 소비하는 것보다 지금 소비하는 것을 더 좋아합니다. 다른 차이가 없다면 즉시 욕구가 만족되기를 원합니다.
마지막으로 위험(risk) 요소가 있기 때문입니다. 인플레이션도 없고, 생산기회도 없다 하더라도 내년에 1000만 원을 받기 전에 전쟁이 날 수도 있는 것이고 기타 여러 가지 불확실한 요소가 있습니다. 따라서 오늘의 1000만 원을 더 선호합니다.
이와 같은 이유로 자본주의 사회의 합리적 인간은 내년에 1000만 원 받는 것보다는 오늘 1000만 원 받는 쪽을 택합니다. 오늘 1000만 원은 내년 1000만 원보다 더 선호되며 더 가치가 커집니다. 이 때 오늘 1000만 원과 내년 1000만 원 사이의 가치의 차이를 이자라고 할 수 있습니다.[1] 내년에 (1000만 원 + 이자)를 제공한다면 오늘 1000만 원을 택하지 않을 사람도 있기 때문입니다.
그러므로 이자율이 화폐의 시간가치를 결정하는 데 중요한 역할을 합니다.
위 내용을 식으로 써봅시다. 현재가치를 PV라 하고 미래가치를 FV라 하면 다음과 같은 관계가 성립합니다.
FV = PV + (PV x r)
r은 이자율입니다. (편의상 연이율로 생각합시다) 위의 식은,
[미래가치 = 현재가치 + 이자]의 의미로 설명한 그대로입니다. 이 식에서 공통인수 PV를 묶어내면,
FV = PV(1+r)
이 됩니다. 이것은 중고등학교 수학시간에 복리를 배우면서 배우는 내용입니다.
같은 방식으로 2년째의 FV는 어떻게 될까요? (1년째 FV) x r한 만큼의 이자가 더 붙을 것이므로,
FV = PV(1+r) + PV(1+r)r
이 됩니다. 역시 공통인수 PV(1+r)을 묶어 내면,
FV = PV(1+r)(1+r)
이 되어서,
FV = PV(1+r)2
이 됩니다. 마찬가지로 3년, 4년 계속 해보면, 일반식은,
FV = PV(1+r)n
이 됩니다.(수학적 귀납법으로 증명을 해야 합니다만.)
따라서 현재가치 PV는 이렇게 됩니다.
PV = FV/(1+r)n
그러면 현재가치와 미래가치에 대해서 실제 예를 들어서 자세히 알아봅시다.
[1] 케인즈는 이자의 의미를 화폐의 유동성에서 찾았습니다. 현재의 현금을 포기하고 채권이나 주식에 투자한다는 것은 더 낮은 유동성을 택하는 것이므로 그에 대한 보상을 요구하는 것이라고 생각했습니다. 이것을 유동성선호(liquidity preference) 이론이라고 합니다.
미래가치(FV, Future Value)와 복리(Compound Interest)
현재의 100만원이 연이율 10%일 때 5년 뒤 어느 정도의 가치를 갖게 될까요?
식으로 써보면,
FV = 100(1+0.1)5 = 100 x 1.6105 = 161.05
161.05만원입니다.
그렇다면 만약 이자를 6개월 마다 5%씩 준다면 어떻게 될까요?
년리 10%인 것은 마찬가지이지만 이자에 또 다시 이자가 붙는 복리이므로 더 큰 액수가 나옵니다.
첫 반 년에 받을 액수는 100(1+0.05)입니다.
그 다음 반 년째에는 원금 100(1+0.05)에 이율 0.05가 다시 곱해지므로,
원리합계는 100(1+0.05) + 100(1+0.05)x0.05가 되어서,
공통인수 100(1+0.05)을 묶어내면, 100(1+0.05)(1+0.05)가 됩니다.
즉, 100(1+0.05)2이 됩니다.
같은 방식으로 1년6개월째, 2년째를 계속 해보면,100(1+0.05)3, 100(1+0.05)4,...의 형태가 된다는 것을 알 수 있습니다.
그러므로 5년째까지 횟수로 10회가 되니까, FV = 100(1+0.05)10이 되어서 이 값은 계산해보면 161.05보다 큽니다.
이것을 일반화해 볼까요?
원금이 P이고, 연이율이 r, 만기가 n인 복리식 예금을 생각해 봅시다.
n년째에 받게 되는 원리합계는 P(1+r)n입니다.
그런데, 반 년에 r/2 이율씩 계산하면 어떻게 되나요?
반 년 후에는 P(1+r/2), 1년 후에는 P(1+r/2)2,... 식으로 되는데,
1년이 2로 나누어졌으므로 n년까지는 2n이 됩니다. 따라서 n년 째에는 P(1+r/2)2n이 됩니다.
같은 이율이라도 이자를 주는 기간을 계속 나누면 다음과 같이 됩니다.
FV = P(1+r/m)nm
연이율 r을 나누는 값 m이 n에도 곱해지는 형태입니다.
이제 이자를 주는 주기를 무한히 줄이면 어떻게 될 지 생각해 봅시다. 주기를 계속 줄이는 것은 위 식에서 m이 무한대로 가는 경우이므로, 극한을 이용해서 계산할 수 있습니다. r/m = 1/z로 치환을 하면,
r/m = 1/z
m = rz
그러므로 위의 FV는 다음과 같이 다시 쓸 수 있습니다.
FV = P(1+1/z)zrn
따라서 아래와 같이 계산됩니다. r은 상수이므로, m이 무한대로 가면 z도 무한대로 갑니다.
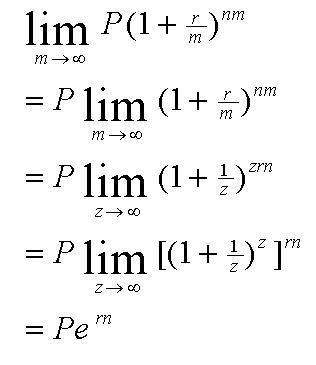
lim (1+1/z)z이 자연상수 e가 되므로 위와 같이 됩니다. 원금 100만원, 복리 10%일 때 이자를 주는 주기를 무한히 줄인 경우 5년 후에 100만 x e0.1x5의 미래가치를 갖습니다.
복리와 관련된 이자율 중에 유효이자율이 있습니다. 유효이자율이란 복리식으로 지급받은 실제 이자를 원금으로 나눈 값입니다. 즉,
유효이자율
= 복리로 받은 이자 총합 / 원금
= (P(1+r)n - P)/P
=(1+r)n - 1
입니다. 이 값은 기간이 1기간보다 크면 "복리 r"에서의 r보다 더 큽니다.[2]
"복리 10%로 10년 후..."에서 받게 되는 실제 이율(=유효이자율)은 10%보다 큽니다.
[2] 기간이 1기간(年)인 경우 n=1이므로, (1+r)-1 = r로 "복리 r"과 똑같습니다. 하지만 n이 1보다 커지면 (1+r)n - 1은 r보다 큰 값을 갖습니다.
현재가치(PV, Present Value)와 연금의 현재가치
이번에는 반대로, 년리 10%일 때 5년 뒤의 161.05 만원이 지금 얼마의 가치를 가질 지 생각해 봅시다.
161.05 = pv(1+0.1)5
이므로,
pv = 161.05/(1+0.1)5
입니다. 100만 원입니다.
미래 현금흐름이 여러 번에 걸쳐서 나타난 경우의 현재가치는 어떻게 될까요?

위와 같이 됩니다. 이 때 C1은 현시점으로부터 1기간 후에 발생하는 현금을 얘기하는 것이고,
i는 이자율입니다. 시그마가 나오고 복잡해 보이지만 자세히 보면,
C1/(1+i) + C2/(1+i)2 + ... + Cn/(1+I)n
이므로, 미래에 발생할 모든 현금흐름의 현재가치를 합쳐준 것입니다.
특히 일정 기간 동안 같은 액수의 현금을 계속 지급해 주는 것을 연금(annuity)이라 합니다.
즉, 위 식에서 C가 일정하다면, 위 식은 연금의 현재가치를 구한 식입니다. 연금의 현재가치 계산법 중 우리 실생활에서 자주 쓰이는 것이 영구연금의 가치 계산입니다. 영구연금이란 사망할 때까지 매기간 일정한 금액이 나오는 것입니다.
영구현금의 현재가치를 식으로 써보면, PV = c/(1+i) + c/(1+i)2 + ... 형태가 되고,
이것은 초항이 c/(1+i)이고 공비가 1/(1+i)인 무한등비급수이므로 아주 쉽게 계산을 할 수 있습니다. 무한등비급수의 합은 고교 수학시간에 배운 대로 S = a/(1-R)입니다. a는 초항, R은 공비입니다.
그러므로 위 식에서 현재가치 PV는,
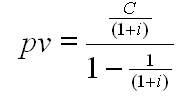
가 될 것이고, 분자, 분모에 (1+i)를 곱해서 정리하면,
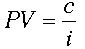
가 됩니다. 외워두면 좋겠죠? 연금액수를 연이율로 나누면 영구연금의 현재가치가 나옵니다.
예를 들어, 금리 수준이 항상 5%이고, 매년 1000만원씩 받는 영구연금이 있다면 이것의 현재가치는,
PV = 10000000/0.05
이 되어서, 2억 원이 됩니다.
연이율이 5%라면, 지금 2억을 받는 것과 매년 1000만원씩 사망할 때까지 받는 것이 똑같은 가치를 갖습니다.
조금 더 응용된 형태의 영구연금 문제를 풀어봅시다.
퇴직후 10년째부터 영구연금을 받는다면 그 연금의 현재가치는 얼마가 될까요?
이 때는 9년 시점에서 영구연금의 현재가치를 구한 다음, 이것을 다시 현재 시점의 현재가치로 환산하면 됩니다.
PV = c/i x 1/(1+i)9
이 됩니다.
'경영:경제' 카테고리의 다른 글
| [재무관리학] 주식의 가치(common stock valuation) (0) | 2020.07.17 |
|---|---|
| [경제학] 생산비용과 이윤극대화(profit maximization) (1) | 2020.07.17 |
| [경제학] 공유지의 비극 (The Tragedy of the Commons) (0) | 2020.07.17 |
| [경영서적] 피터 드러커(Peter Drucker)의 효과적인 의사결정 (0) | 2020.07.17 |
| [경영서적] 피터 드러커(Peter Drucker)의 우선 순위 결정 (0) | 2020.07.17 |
