티스토리 뷰
채권의 가치는 미래에 받을 쿠폰과 원금의 현재가치를 합한 것이라고 했습니다. 이 글에서는 채권의 수익율에 대해 조금 더 자세히 알아 봅시다. 채권의 수익율은 크게 만기수익율, 단순수익율, 실효수익율이 있습니다.
만기수익율(YTM; Yield To Maturity; 유통수익율)
만기수익율은 유통수익율이라고도 하며 일반적인 채권수익율입니다. 만기수익율을 이해하기 위해서, 채권의 현재가치 식을 다시 한 번 써봅시다.

쿠폰(C=액면가 x 쿠폰이율)만큼의 이자를 매기 지급받고 만기에는 액면가 F를 지급받으므로 위와 같이 현재가치로 환산해서 합한 것이 채권의 현재가치, 즉 현재 채권의 가격이 됩니다. 위 식에서의 수익율 r을 만기수익율(YTM; Yield To Maturity)이라 합니다. P0의 가격에 구입해서 만기까지 보유했을 때 얻게 되는 수익율이기 때문입니다. 투자액 P0와 채권으로부터 발생하는 미래 현금흐름(=쿠폰+원금)의 현재가치를 일치시키는 가격이므로 일종의 내부수익율(IRR)입니다.
만기수익율(YTM)은 위 식에서 본 것처럼 내부수익율(IRR)과 같은 개념이므로, 재투자수익율이 일정하다는 가정하에 계산됩니다. 즉, 쿠폰을 받은 뒤 그것을 다시 같은 수익율의 투자처에 재투자했을 때의 수익율입니다.
어떤 회사의 회사채가 액면가 10,000원, 만기 5년에 이표이자율 8%인데 시장에서 9000원에 거래된다고 하면 이 채권의 만기수익율은 다음과 같이 계산됩니다.
9000 = 800/(1+r) + 800/(1+r)2 + ... + 800/(1+r)5 + 10000/(1+r)5
내부수익율 IRR을 구하는 것과 똑같죠? 이것을 계산해 보면 r=10.684%입니다. 쿠폰으로 받은 800원이 다시 8%의 수익율로 복리처럼 재투자되기 때문에 8%보다 큰 10.68%의 수익율이 나옵니다.[1]
회사채의 경우는 일반적으로 이자가 매 분기마다 지급되므로 화폐의 시간가치와 복리에서 알아 본 것처럼, (쿠폰/4)만큼의 이자를 (만기x4) 기간 동안 지급받는 것으로 계산하면 됩니다. 예컨데, 위 회사채의 경우 분기마다 쿠폰이 지급된다면 다음과 같이 만기수익율을 구할 수 있습니다.
9000 = 200/(1+r) + 200/(1+r)2 + ... + 200/(1+r)20 +1000/(1+r)20
물론 이렇게 구한 r에 다시 4를 곱해야 연수익율이 됩니다. 만기수익율은 위 식에서 본 것처럼, 채권 가격이 오르고 내림에 따라, 또 만기까지 얼마나 남았느냐에 따라 바뀝니다.
단순수익율(Current Yield; 경상수익율)
단순수익율은 경상수익율이라고도 하며, 간편하게 계산되는데 반해 정확성은 조금 떨어집니다. 단순수익율은 채권의 '현재' 수익율을 구하는 것으로, 쿠폰액을 현재 채권가격으로 나눠서 계산하면 됩니다.
Current Yield = (C/P) x 100
위에서 예로 들었던 회사채의 경우, 연간 쿠폰이 800원이고 현재 채권가격이 9000원이므로,
Current Yield = 800/9000 = 8.89%
입니다. 단순수익율은 식에서 본 것처럼 미래에 받을 쿠폰에 대한 화폐의 시간가치가 고려되지 않았고 또 자본소득, 즉 채권을 액면가보다 비싸게 또는 싸게 산 데서 비롯되는 수익율을 고려하고 있지 않으므로 정확성이 떨어집니다만 계산이 간편하므로 종종 사용됩니다.
실효수익율(Effective Rate of Return)과 연평균수익율, 발행수익율
실효수익율을 이해하기 위해서는 먼저 총수익과 연평균수익율을 알고 있어야 합니다.
총수익이란 채권투자로부터 비롯되는 수익을 모두 합한 값입니다. 이표채라면 모든 쿠폰과 만기시 받을 액면가를 합한 게 될 것이고 할인채라면 만기시 받을 액면가가 채권의 총수익이 될 것입니다. 예컨데, 이표이자율(표면금리) 8%인 액면가 10,000원의 3년 만기 회사채의 총수익은 화폐의 시간가치와 복리에서 공부해 본 것처럼 이렇게 계산하면 됩니다.
10000(1+0.08)3 = 12,597
따라서 총수익율은 {(12,597-10,000)/10,000} x 100 = 26%입니다.
연평균수익율이란 총수익율을 연 단위로 계산한 것입니다. 위의 경우 3년이므로, 26%/3 = 8.67%입니다.
이제, 조금 어려운, 실효수익율에 대해 알아 봅시다. 실효수익율은 복리의 유효이자율처럼, 앞으로 받게 될 쿠폰, 쿠폰의 재투자수익, 되돌려 받을 투자원금을 모두 다 합한 것을 투자원금으로 나눈 것입니다. 문자 그대로 투자액 대비 실제로 거둬들이는 수익의 비율을 파악하는 것입니다. 즉, 복리에서의 유효이자율과 같은 개념입니다. 그러므로 FV를 채권으로부터 얻을 수 있는 미래 수익의 총합, P를 채권의 현재가격이라 하면 실효수익율 R은 다음과 같이 구할 수 있습니다.
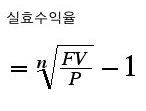
FV는 미래의 쿠폰, 쿠폰의 재투자수익, 만기에 돌려 받을 투자원금을 모두 합한 것입니다..
위 회사채를 발행 당시 구입해서 만기까지 보유한 경우 실효수익율을 구해 보면,

이므로, 약 8%라는 것을 알 수 있습니다. 이처럼 채권에서 발생하는 모든 미래현금을 종합적으로 고려한 수익율이므로 채권투자에서는 실효수익율을 비교하는 것이 더 합리적이라고 볼 수 있습니다.
할인채의 실효수익율은 발행수익율이라고도 합니다. 예를 들어, 3년 만기 산업금융채권이 표면이율 3.09%, 액면가 10,000원으로 발행되었다면 이 채권의 발행수익율은 다음과 같이 계산됩니다.
매출가액 = 10,000 - (309 x 3) = 9,073원
이므로 발행수익율은,

연 실효수익율은 복리의 유효이자율과 같은 의미이므로 다른 방식으로 구해볼 수도 있습니다. 매분기마다 쿠폰을 지급하는 3년 만기 산금채의 표면금리가 3.26%라면 이 채권의 연 실효수익율은 어떻게 구할 수 있을까요? 단, 재투자수익율도 3.26%라고 가정합니다.
이것은 3개월마다 (3.26/4)%의 복리를 받는 것의 유효이자율을 구하는 것이므로, 연간 복리로 받을 이자 총합의 원금에 대한 수익율을 구하면 됩니다.
{1+(0.0326/4)}4 - 1 =1.03300 - 1 = 0.03300 = 3.30%
만약 같은 금리인데 연 2회 이자를 지급하는 경우라면 이 채권의 연 실효수익율은,
{1+(0.0326/2)}2 - 1 = 1.032865 - 1 = 0.032865 = 3.29%
연 실효수익율이므로 만기는 3년이지만 연간 이자지급횟수인 제곱, 네제곱을 하고 있다는 것에 주의하세요.
이상 수익율은 모두 세전수익율로 이자소득에 대한 세금이 고려되지 않은 것입니다. 세후수익율은 이자소득에서 세금을 제한 뒤에 똑같이 계산하면 됩니다.
채권 수익율 예제
다른 투자안과 달리 채권의 경우 여러 종류의 수익율이 사용되고 있어서 무척 혼란스러워 보입니다. 하지만 위의 세 가지 수익율의 개념만 잘 파악하고 있으면 대부분의 경우 큰 문제 없이 채권 투자의 타당성을 분석할 수 있습니다. 정확한 이해를 했는지 확인하기 위해 다음의 예제를 직접 풀어 보세요.
1. 액면가 10,000원, 표면금리가 연 3.05%인 만기 1년의 산금채가 할인채인 경우 발행수익율은 얼마입니까?
2. 액면가 10,000원, 표면금리가 연 3.36%인 만기 5년의 복리채를 구입해서 만기까지 보유한 경우 연평균 수익율은 얼마입니까?
3. 액면가 10,000원, 이표금리가 8%인 3년 만기 회사채가 9,000원에 거래되고 있습니다. 이 채권의 만기수익율은 얼마인가요?
마지막으로 조금 까다로운 문제입니다.
4. 1년 만기 6개월 후급, 표면금리 12%의 이표채를 액면가에 구입해서 1년간 보유했을 때 실효수익율은 얼마입니까? 단, 재투자수익율은 10%입니다.
[1] 참고로 , 만기수익율을 휴렛팩커드12C 재무계산기(HP 12C Financial Calculator)로 계산하려면 어떻게 해야 하는지 알아 봅시다. 유통되는 중간에 구입한 경우는 구입한 날짜와 만기일을 직접 입력해서 [f->YTM] 버튼을 이용합니다만 여기서는 편의상 발행당시 구입해서 만기까지 보유한 경우 어떻게 계산하는지를 설명합니다.
YTM은 IRR을 구하는 것과 똑같으므로, PV에 현재 채권가격, FV는 만기에 받을 액면가, PMT에 쿠폰, n에 만기까지 이자지급 횟수를 입력한 뒤 i를 구하면 됩니다. 위 예의 경우 다음과 같은 순서로 키를 누르면 되겠죠.
f->CLx
9000->CHS->PV
800->PMT
10000->FV
5->n
i (running...)
i=10.684
'경영:경제' 카테고리의 다른 글
| 시장구조 [3] 과점시장 (Oligopoly) (0) | 2020.06.22 |
|---|---|
| 시장구조 [2] 독점시장(Monopoly) (1) | 2020.06.22 |
| 시장구조 [1] 완전경쟁시장 (Perfect Competition) (0) | 2020.06.22 |
| 국제 금융 시스템(IMS)의 간략한 역사 (0) | 2020.06.20 |
| [재무관리학] 채권의 가치 (0) | 2020.06.18 |
