티스토리 뷰
코넬 대학교 Jon Kleinberg 교수의 논문, "Authoritative Sources in a Hyperlinked Environment" 소개
2003-4-15
개괄
논문의 도입부에서는 질의어와 'authoratative sources'의 관계, 그리고 링크 구조의 분석 방법 등을 다룹니다. 우선 "broad search topic"이란 문구가 나오는데, 검색어는 주제의 범위가 넓은 것과 특화된 것이 있습니다. 예를 들어 "학교"라는 검색어는 대단히 광범위한 검색어로 많은 결과가 리턴됩니다. 반면 "정보검색"이라는 질의어는 매우 특별한 것으로 결과로 반환되는 것이 훨씬 적습니다. "Hubs and authorites"라는 링크 구조 모델을 다루는 본 논문에서 소개하는 알고리듬은 전자와 같은 광범위한 검색 키워드에 대한 검색결과를 어떻게 링크 구조를 이용해서 정제할 수 있을까를 모색해 본 것입니다. 범위가 넓은 주제에 대한 검색 결과중 어떤 것이 가장 권위 있는 페이지인지를 찾아내는 방법을 생각해 보는 것입니다.
우리가 어떤 검색을 했을 때 결과로 반환되는 페이지가 좋은 결과라고 판단하는 것은 주관적입니다. 검색 결과의 품질에 대한 평가는 지극히 주관적이기 때문에 그 결과가 검색어와 관련 있다, 없다를 판단하는 데 있어서 인간의 판단이 배제된 어떤 객관적인 기준, 나아가서 알고리듬으로 구현할 수 있을 만큼 공식화된 방법을 찾아낼 필요가 있습니다. 이 부분을 무시한 채 검색 속도나 저장 효율만 관심을 갖는 것은 부수적인 부분에 집중하는 것일 수 있습니다. 어떤 페이지가 검색어와 관련된 페이지이고 그 관련된 페이지 중 어떤 것이 좋은 페이지인가를 판단하는 객관적인 방법을 찾는 것이 훨씬 중요하다고 할 수 있고 이 논문은 그 부분에 대한 하나의 방법을 제공하고 있습니다.
"authority"란 무엇인가?
검색어는 특화된 것이 있고 광범위한 것이 있다고 했습니다. 예를 들어, "펄에서 url을 인코딩하는 데 사용되는 모듈은?" 같은 질의어는 대단히 특화된 것입니다. 반면, "자바 프로그래밍 언어에 관한 정보"는 광범위합니다. 전자와 같은 질의어는 희소성 문제가 생깁니다. 해당 정보를 담고 있는 페이지 수가 매우 적은 데서 비롯되는 문제입니다. 후자는 과다성 문제가 생깁니다. 관련되는 페이지가 너무 많아서 문제가 됩니다. 과다성 문제가 생기는 경우 인간이 처리할 수 있는 수준을 넘어선 양의 정보가 제공되기 때문에 그 결과들 중 어떤 것이 가장 권위 있고 좋은 페이지인지 찾아낼 방법이 있어야 합니다.
그렇다면 권위 있다는 것은 어떤 의미일까요? 예를 들어 검색어로 "harvard"를 입력하면 수만, 수십만 페이지가 결과로 나오겠지만 그 중 가장 권위 있는 페이지는 당연히 하버드 대학교 홈페이지인 www.harvard.edu일 것입니다. 그런데 이런 권위 있는 페이지를 찾아낼 수 있는 문서 내부의 특성이 없습니다.
예컨데 단어 빈도수를 생각해 봅시다. www.harvard.edu는 "harvard"라는 단어가 가장 많이 등장하는 페이지가 아닐 것입니다. 단어 빈도수만을 기준으로 권위를 추정하는 경우 전혀 엉뚱한 페이지가 선택될 수 있습니다. url은 어떨까요? 위 경우는 ".edu"가 들어간 것 중 "harvard"가 들어간 페이지를 찾으면 해당은 되겠습니다만 모든 검색어에 일반적으로 적용할 수 있는 방법은 아닙니다. url 자체가 권위를 판단하는데 힌트를 주기 힘듭니다. 문서의 길이는 어떨까요? 그것도 별로 효과가 없습니다. 검색 결과 중 긴 페이지를 찾는다고 반드시 그 페이지가 권위가 있느냐면 그렇지 않을 가능성이 훨씬 높습니다.문서 내부적인 정보만으로는 어떤 페이지가 권위있는 곳이다 아니다를 판단하기가 쉽지 않습니다.
하나 더 예를 들어 봅시다. "검색 엔진"이라는 질의어에 대한 결과 중 권위 있는 곳은 네이버라든지 구글, 다음 등입니다. 그런데 이들 페이지가 질의어 "검색 엔진"과 어떤 관련성을 갖나요? "검색 엔진"이라는 단어가 가장 많이 등장하는 것도 아니고 특별히 문서 자체에서 이들의 권위를 유추해 낼 방법이 없습니다. 그렇다면 검색창에 "검색 엔진"이라고 입력을 했을 때 어떻게 하면 위와 같은 권위 있는 곳을 찾아낼 수 있을까요? 오쏘리티를 찾겠다는 것은 바로 이 문제를 해결할 방법을 찾는 것입니다. 검색어에 대한 검색 결과 중 어떤 것이 가장 좋은 페이지인가를 판단해 보겠다는 것이고 그런 페이지를 오쏘리티(authority)라 하는 것입니다.
하이퍼링크가 해결책
위 문제를 해결하는 중요한 수단 중 하나가 하이퍼링크(hyperlink)입니다. 하이퍼링크는 사람의 판단이 포함되어 있습니다. 웹 페이지를 만드는 사람이 특정 페이지를 링크하는 것은 그 페이지가 좋은 페이지이기 때문일 가능성이 큽니다. 링크할 것인가 말 것인가에는 인간 판단이 인코딩되어 있는 것입니다. 그러므로 링크는 오쏘리티를 찾는 데 큰 도움이 될 수 있습니다.
다른 곳에서 링크가 많이 되어 있는 페이지는 가치가 큰 페이지일 가능성이 높습니다. 또 하나 링크를 활용하는 것의 장점은 문서의 우수성을 판단할 기준이 문서 내에 담겨있지 않아도 상관없다는 점입니다. 그 문서가 길든 짧든, 질의어와 매치된 단어가 많든 적든 그 문서의 우수성을 판단하는 데 도움이 됩니다.
링크도 물론 문제는 있습니다. 예컨데 특정 목적을 가지고 링크를 하는 경우도 많습니다. 광고성 링크, 내부 네비게이션 링크 등이 그렇습니다.
HITS 알고리듬
HITS 알고리듬은 크게 2단계로 나뉩니다. 먼저 질의어와 관계있는 페이지들의 부분집합(서브 그래프(subgraph))을 만드는 단계입니다. 그 다음에는 만들어진 서브 그래프를 이용해서 헙(hub)과 오쏘리티(authorities)를 계산하는 단계입니다.
1. 서브그래프(subgraph) 만들기
하이퍼링크로 연결된 페이지들의 컬렉션 V를 G = (V,E)라는 directed graph로 표현해 봅시다. 이 때 각 노드는 페이지에 해당하고 (p,q) ∈ E는 p에서 q로의 링크가 있다는 것을 뜻합니다. 그리고,
(1) 노드 p의 out-degree: 밖으로 나가는 링크의 갯수
(2) 노드 p의 in-degree : 노드 p를 가리키는 링크의 갯수
(3) G[W] : V에 속하는 부분집합 W로부터 만든 그래프
(4) 질의어 : σ라고 합시다.
이제 광범위 검색 주제어인 질의어 σ에 대한 오쏘리티를 링크 구조만을 이용해서 어떻게 찾을 수 있는지 생각해 봅시다. 질의어 σ를 담고 있는 페이지 전체 집합을 Qσ라 합시다. 알고리듬은 이 Qσ를 대상으로 하면 안 됩니다. 그 이유는 첫째, 질의어를 담고 있는 페이지는 아마도 수백만 페이지 이상일 것이기 때문에 computationally expensive합니다. 둘째, 앞에서 얘기한 것처럼 중요한 오쏘리티는 질의어 자체를 담고 있지 않은 경우도 많습니다. 우리가 원하는 집합을 Sσ라 하면, Sσ는 이런 특성을 가지면 좋을 것입니다.
(1) 상대적으로 작아야 한다.
(2) 관계되는 페이지가 많아야 한다.
(3) 대부분의 오쏘리티를 담고 있으면 좋겠다.
알고리듬의 첫 단계인 서브 그래프를 만드는 단계는 이런 특징을 갖는 Sσ를 찾아내는 것입니다. 그러면 Sσ를 어떻게 찾아낼까요?
일반적인 텍스트 기반 검색엔진에 질의어를 넣었을 때 결과 중 상위 t개의 페이지를 루트셋(root set) Rσ라 합시다. 이 Rσ는 아마도 위의 조건 중 1, 2번은 만족하지만 3번은 만족하지 않을 수 있습니다. 그러므로 Rσ를 이용해서 강한 오쏘리티(strong authorities)를 찾아낼 수 있다면 우리가 원하는 Sσ에 가까운 서브 그래프를 만들어 낼 수 있을 것입니다.
그런데 오쏘리티는 Rσ에 있는 페이지들이 가리키는 페이지들 중에 많이 존재할 가능성이 높습니다. 관계되는 페이지들이 가리키고 있는 페이지는 권위 있는 페이지일 가능성이 크기 때문입니다. 따라서 Rσ를 링크를 이용해서 확장하면 우리가 원하는 강력한 오쏘리티가 들어있으면서, 작고, 관계성 높은 서브 그래프를 만들어 낼 수 있을 것입니다. 이것을 알고리듬으로 표현하면 이렇게 됩니다.
Subgraph(σ, ε, t, d)
σ : a query string
ε : a text-based search engin
t,d : natural numbers
Let Rσ denote the top t results of ε and σ
Set Sσ := Rσ
For each page p ∈ Rσ
Let T+(p) denote the set of all pages p points to
Let T-(p) denote the set of all pages pointing to p
Add all pages T+(p) to Sσ
If |T-(p)| ≤ d then
Add all pages in T-(p) to Sσ
Else
Add an arbituray set of d pages from T-(p) to Sσ
End
Return Sσ
T-(p)가 d보다 작거나 같을 때 이것을 Sσ에 포함시킨다는 부분을 조금 생각해 봐야 합니다. T-(p)중 몇 개만을 취한 까닭은 무엇일까요? 만약 Rσ에 구글 홈페이지가 들어있다고 해 봅시다. 그러면 구글 홈페이지를 가리키는 페이지는 수백, 수천만 개 이상일 것이기 때문에 이들을 다 포함시키는 경우 Sσ가 턱없이 커집니다. 그러므로 일정한 개수만 포함시키는 것입니다.
위와 같은 과정을 통해서 얻어낸 Sσ를 "σ의 base set"이라고 합시다. 이 베이스 셋을 구하기 위해 이 논문에서는 검색 엔진으로는 알타비스타를 사용했고 t=200, d=50으로 했습니다. 이렇게 했을 때 대략 1000 ~ 5000개 정도의 페이지를 담고 있는 Sσ가 만들어졌다고 합니다.
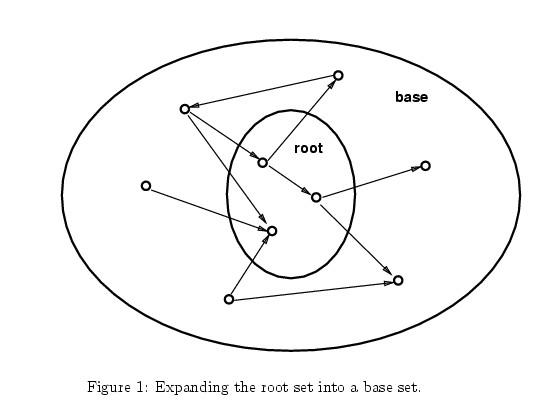
이렇게 얻어진 서브그래프는 몇가지 휴리스틱스를 적용함으로써 조금 더 줄일 수 있습니다. 예를 들어, 순수하게 네비게이션의 용도로만 쓰이는 링크는 권위를 부여하는 기능이 없으므로 배제할 수 있습니다. 도메인 네임을 살펴 봐서 동일한 곳에서 동일한 곳으로 연결되고 있는 링크는 네비게이션 목적일 가능성이 높으므로 제외합니다. 또는 한 도메인 내의 많은 페이지가 외부의 어떤 한 페이지로만 링크가 되고 있는 경우도 광고성 링크거나 특별히 트래픽을 몰아 줄 계약을 체결했을 가능성이 있습니다. 이런 것을 제외하기 위해 단일 도메인에서 특정 페이지 p로의 링크가 있는 페이지의 갯수는 4개 ~ 8개로 제한합니다.
2. 허브(hub), 오쏘리티(authority) 계산
앞 단계에서 만든 서브그래프를 이용, 이제 우리가 최종적으로 구하고자 하는 허브(hubs)와 오쏘리티(authorities)를 찾아냅니다. 일단 Sσ를 그래프화 한것을 Gσ라 합시다. 이제 링크 구조를 이용해서 이 Gσ 속에 존재하는 허브와 오쏘리티를 찾아내는데, 제일 쉽게 생각해 볼 수 있는 것이 Gσ 내의 페이지들을 in-degree 순으로 정렬하는 것입니다. 이것은 직관적으로 좋은 방법일 것 같습니다. 일단 Gσ라는 특정 검색어와 관계성이 높은 페이지 집합 속에서 다른 페이지로부터의 링크가 많다는 것은 그 만큼 좋은 페이지일 가능성이 높기 때문입니다. 하지만 실제로 해보면 강력한 오쏘리티와 보편적으로 인기가 높은 페이지(universally popular pages) 사이의 긴장이라는 문제가 생깁니다. 예를 들어 "java"라는 질의어의 경우 www.gamelan.com과 java.sun.com이라는 결과와 함께 캐리비안 휴양 관련 사이트와 아마존 홈 페이지가 함께 순위권에 듭니다. 이것은 특정 주제에 관한 오쏘리티와 함께 주제에 관계없이 링크가 많이 된(universally popular) 것이 존재하기 때문입니다. 이 문제의 해결책은 페이지의 텍스트 내용도 감안해서 검색어와 매칭되는 단어가 등장하는 것을 골라낸다 정도가 될 것인데 이것도 실제로 해보면 별로 효과가 없다고 합니다.
오히려 논문의 저자는 순수하게 링크 구조만을 활용해서 이 문제를 해결할 수가 있다고 하는데요. 그 출발점은 이렇습니다.
"모든 오쏘리티들은 큰 in-degree를 갖는다는 점과 함께 그 오쏘리티들을 가리키고 있는 페이지들 역시 중복된다는 공통점을 갖는다."
어떤 주제에 관한 오쏘리티들을 많이 링크하고 있는 페이지를 중심축 역할을 한다는 의미에서 허브(hub)라고 명명합시다. 그러면 앞의 기술은, "좋은 오쏘리티들은 in-degree가 높다는 점과 함께 많은 허브들로부터 링크되어 있다는 공통점이 있다."는 얘기가 됩니다. 여러 허브들로부터 링크되어 있을수록 좋은 오쏘리티가 되며 여러 오쏘리티를 링크하고 있을수록 좋은 허브가 되는 것입니다. 허브와 오쏘리티는 상호강화적인 관계(mutually reinforcing relationship)입니다.
그러므로 좋은 오쏘리티는 좋은 허브를 찾는 것을 통해서 찾아낼 수 있고, 좋은 허브는 좋은 오쏘리티를 통해서 찾아낼 수 있습니다. 그리고 이들 허브와 오쏘리티는 광범위적 질의어의 검색 결과 중에서도 특별히 좋은 페이지로 생각해 볼 수 있는 것입니다.
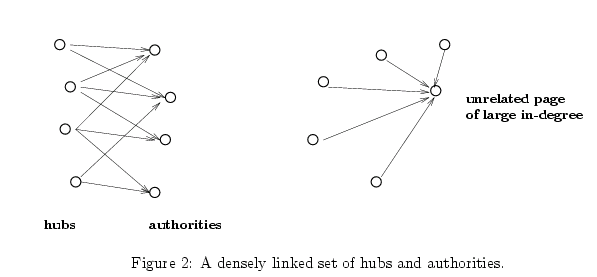
위에서 살펴본 내용을 이제 수학적으로 기술해 봅시다.
"authority weight", 즉 오쏘리티 가중치를(높을수록 좋은 오쏘리티) x(p)라 하고, "hub weight", 허브 가중치를(높을수록 좋은 허브) y(p)라 하면 다음과 같은 두 가지의 연산을 생각해 볼 수 있습니다.
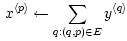

q-->p로의 링크가 있을 때 p 페이지의 오쏘리티 가중치는 q 페이지들의 허브 가중치 y(p)를 모두 합한 것입니다.
p-->q로의 링크가 있을 때 p 페이지의 헙 가중치는 q 페이지의 오쏘리티 가중치 x(q)를 모두 합한 것입니다. 이것은 반복 알고리듬(iterative algorithm)이기 때문에 이터레이션을 시켜서 계산해야 합니다. 반복 연산을 했을 때 어떤 일정한 값으로 수렴하면서 균형을 이루는지 알아보는 것입니다. 그리고 수렴해서 일정한 값을 갖는다면 각 페이지들의 최종 허브 가중치와 오쏘리티 가중치를 알게 될 것입니다. 어떤 페이지가 얼마나 좋은 허브인지, 얼마나 좋은 오쏘리티인지를 알 수 있는 것입니다.
이것을 알고리듬 형태로 표시해 봅시다.
x(p)의 집합 {x(p)}를 벡터 x라 하고, y(p)의 집합 {y(p)}를 벡터 y라 하면,
Iterate(G,k)
G : a collection of n linked pages
k : a natural number
Let z denote the vector (1,1,1,...,1) ∈ Rn.
Set x0 := z.
Set y0 := z.
For i = 1,2,...,k
Apply I operation to (xi-1, yi-1), obtaining new x-weights x'i.
Apply O operation to (x'i, yi-1), obtaining new y-weights y'i.
Normalize x'i, obtaining xi.
Normalize y'i, obtaining yi.
End
Return (xk, yk).
처음에는 모든 페이지에 대해 허브 가중치, 오쏘리티 가중치를 1로 해서 I operation을 시행한 다음 얻은 새로운 x'를 이용, 이번에는 O operation (x만 x'i 이고 y 는 i-1 이라는 점에 주목하세요.)을 시행해서 새로운 y'을 얻고 이를 노멀라이징한 다음 다시 반복합니다. 언제까지? 우리가 정한 k번까지로 되어 있습니다. 알고리듬 자체는 아주 단순한 것입니다. 이 때 노멀라이징하는 방법으로 이 논문에서는,
∑ x(p)2 = 1
∑y(p)2 = 1
을 사용했습니다. 위에서 최종적으로 얻은 벡터 x의 각 원소는 각 페이지의 오쏘리티 가중치입니다. 벡터 y의 각 원소는 각 페이지의 헙 가중치를 가리킨다는 점을 주목해야 합니다. 그리고, k값을 상당히 크게 해서 이터레이션을 계속 시키면 x, y 모두 일정한 값으로 수렴합니다. 일정한 값으로 안정이 되고 나서 얻은 xk, yk 중에서 각각 상위 c개씩을 뽑아 내면 이들이 바로 우리가 찾는 좋은 허브와 좋은 오쏘리티가 되는 것입니다.
이 알고리듬을 실제 구현해서 그 결과를 싣고 있는데 상당히 인상적입니다. 예를 들어, "Gates"라는 검색어에 대해서 상위 3개의 오쏘리티는,
http://www.roadahead.com/ , http://www.microsoft.com/, http://www.microsoft.com/corpinfo/bill-g.html
로 나타났습니다. 순수하게 알타비스타에서 검색한 결과는 http://www.roadahead.com 페이지가 123번째 결과로 나왔다 합니다.
"search engines"라는 검색어에 대해서도 상위 5위까지를 살펴보면,
http://www.yahoo.com/ , http://www.excite.com/ , http://www.mckinley.com/ (Magellan 검색엔진), http://www.lycos.com/, http://www.altavista.digital.com/입니다. 사용자가가 원하는 오쏘리티를 잘 찾아낸다는 것을 알 수 있습니다.
정리해 봅시다. 이 논문을 통해 텍스트적인 정보를 전혀 감안하지 않은, 순수하게 링크 구조만을 사용해도 상당한 수준으로 좋은 페이지를 찾아낼 수 있다는 사실을 알 수 있습니다. 페이지 내부 정보만으로는 퀄리티를 확인하기 힘든 데 반해 하이퍼링크를 이용함으로써 이 문제를 훨씬 객관적으로 해결할 수 있다는 것을 알 수 있습니다.
'테크' 카테고리의 다른 글
| 맥북(Macbook)에 부트캠프(bootcamp) 없이 윈도우즈만 인스톨하려면 (0) | 2020.08.12 |
|---|---|
| TCP/IP 프로토콜(protocol)의 역사와 개요 (0) | 2020.08.08 |
| 오픈 소스 구루, 해커, 리챠드 스톨먼 (Richard Stallman) 인터뷰 (0) | 2020.07.28 |
| GIF와 JPEG (0) | 2020.07.22 |
| 마임 타입 (MIME Type), 미디어 타입(Media Type) 개괄 (0) | 2020.07.21 |
