티스토리 뷰
노동한계생산/자본한계생산 = 노동가격/자본가격
2001-10-21
왜 개인 혼자서 물건을 만들어 팔지 않고 기업이라는 것이 등장하게 되었는지, 기업이라는 형태를 취함으로써 얻는 이점은 어떤 것이 있는가를 생각해 보고 기업의 비용극소화 조건을 공부해 봅시다. 기업의 형태를 취하면 다음과 같은 이점이 있습니다.
기업의 존재의의
1.거래비용(transaction cost)을 낮춘다
기업의 형태를 취하면 R.Coase 교수가 말한 거래비용이 매우 낮아질 수 있습니다. 거래비용은, 무엇인가 사고자 할 때 상품 등을 검색하는 데 소요되는 검색비용, 검색 후 파는 측과 협상을 하는 데 드는 협상비용, 그리고 협상이 완료된 이후 협상대로 정확히 이행되는지를 담보하는 데 드는 비용이 있습니다. 회사 내에 광고를 전담하는 부서가 있다고 생각해 봅시다. 그 경우 제품 광고를 위해 외부 광고 대행사를 찾고(검색비용), 만나서 계약 조건을 협상하고(협상비용), 계약된 대로 잘 만들어 지는지 감시하는 데 비용을 지불할 필요가 없습니다. 이렇게 기업의 형태를 갖추고 그 안에 여러 가지 기능을 통합함으로써 특정 기능이나 상품을 시장에서 구입하는 것에 비해 획기적으로 비용을 낮출 수 있습니다.
거래비용은 기업이 활동할 범위를 결정하는 데도 영향을 미칩니다. 위의 예처럼, 광고 부서를 만드는 쪽이 외부 대행사를 이용하는 것보다 더 거래비용이 낮다면 그 기업은 회사 내에 광고 부서를 만드는 것이 유리합니다. 곧, 그 회사의 활동 범위는 광고까지 포괄합니다. 반대로 부서를 꾸리고 인력을 채용하는 비용이 외부에 아웃소싱을 주는 것보다 더 많은 비용이 소요된다면 그 부문은 기업의 활동 범위에 포함시킬 필요가 없습니다. 광고까지 진출하지는 않는 것입니다. 그러므로 거래비용은 기업의 범위에 영향을 미칩니다. 이렇게 기업이 어떤 시장(산업)에 진출하느냐의 여부를 판단하는 전략을 기업전략(Corporate Strategy)이라고 하며, 기업전략은 거래비용을 감안해서 결정되어야 합니다. 대기업이 지나치게 다양한 부문에 진출하는 것을 비판할 때는 다각화가 거래비용 절감 효과를 가져오는지를 함께 고려해야 합니다.
2. 규모의 경제(Economies of scale)
규모의 경제(Economies of scale)란 거대한 고정비용이 많은 생산량에 의해 분산되어서 많이 만들어 낼수록 평균생산비가 더 떨어지는 것입니다. 기업의 형태를 취해 대량 생산을 해서 규모의 경제 효과를 누리면 낮은 평균생산비에서 비롯되는 강한 원가 경쟁력을 갖게 됩니다. 그것이 두 번째 기업의 존재의의입니다. 볼펜을 생각해 봅시다. 한 개인이 만들어서 판다면 과연 몇 백 원의 가격에 볼펜을 판매할 수 있을까요?
3. 팀 프러덕션
기업은 기능별 분과를 통해 각 부서별 전문화가 가능하므로 더욱 효율적 생산이 가능합니다.
4. 재원조달
개인의 경우 돈을 조달하는 데 한계가 있을 수밖에 없지만, 기업은 개인보다 훨씬 더 다양한 경로를 통해 더 큰 규모의 자금을 손쉽게 조달할 수 있습니다. 회사채를 발행한다든지, 주식 발행을 통해 자금을 조달할 수 있습니다.
기업의 목표: 이윤극대화(profit maximization)
기업 존재의 의의에 관해서는 여러 가지 학설들이 많습니다. 단순히 기업의 주인인 주주의 이익을 늘려주기 위해 기업이 존재한다고만 규정하기엔 기업이 맡고 있는 역할과 책임이 너무 큽니다. '기업의 사회적 책임'이란 표현이 그런 주장을 상징하고 있습니다. 현대의 기업은 주주들에게 경제적 이익을 가져다 줌과 동시에 국민경제의 중요한 주체로서의 역할도 수행하고 있습니다. 많은 직원들을 고용하며 사회적 안정을 뒷받침하고 있고, 이익의 일부를 법인세로 내며 국가경제에 큰 보탬이 되고 있고, 정부의 손길이 미치지 못하는 곳에 재원을 대며 일정한 역할을 하기도 합니다. 특히, 오늘날 기업들은 주식시장을 통해 공개되어 있는 경우가 많아서, 불특정 다수를 주주로 하고 있습니다. 자본시장을 통해 투자를 하고 있는 다수의 주주들간의 이해관계가 복잡하게 얽히면서 기업은 그 이해충돌(conflicts of interest)을 조절하고 균형을 맞춰야 하는 책임까지 갖게 되었습니다. 이렇게 기업을 단순히 주주가치 극대화를 목표로 하는 실체로 생각하지 않고, 정부, 일반 국민(소비자), 임직원, 관련 회사, 채권은행 등과 같은 다양한 이해관계자에게 영향을 미치는 실체로 보는 사고방식을 이해관계자 자본주의(stakeholder's capitalism)라고 합니다. 전자와 같이 주주가치 극대화의 관점을 취하는 사고방식은 주주 자본주의(stockholder's capitalism)라고 하며 미국식 사고입니다. 반면 이해관계자 자본주의는 유럽식 사고방식입니다.
현실적으로는 두 사고체계가 각자의 장단점을 갖고 팽팽히 맞서있지만, 기초적인 경제학적 분석을 함에 있어 기업의 목표는 '주주 가치의 극대화'로 생각합니다.
그러면 주주에게 돌아가는 이윤을 극대화(profit maximization)하려면 어떻게 해야 할까요? 비용은 낮출 수 있는 한 낮추고, 수입은 최대한 높여야 합니다. 그래서 비용 최소화가 어떻게 달성될 수 있는지를 알아보고 있습니다.
비용은 보다 더 자세히 나눌 수 있습니다.
고정비용과 가변비용(fixed cost vs variable cost)
비용에는 고정비용(fixed cost)과 가변비용(variable cost)이 있습니다. 고정비용은 생산량이 늘든 줄든 일정하게 지출되는 비용이고 가변비용은 생산량을 늘리면 그에 따라 같이 늘어나는 비용입니다. 건물 임대료는 일단 계약을 하고 나면 사업이 잘 되든 안 되든 매달 일정액을 냅니다. 고정비용입니다. 반면 볼펜 잉크를 사는 비용은 볼펜 생산량이 늘수록 더 커집니다. 가변비용입니다.
그런데 길게 봐서는 고정비용도 가변비용이 될 수 있습니다. 예를 들어, 현재 있는 건물이 너무 좁고 더 많은 일감을 소화해 내기가 힘들어서 더 큰 건물로 옮겼다고 합시다. 이 경우 건물 임대료도 생산량의 변화에 따라 바뀌는 변동 비용이 됩니다. 고정비용도 어느 시점까지만 고정인 것이지, 장기적 관점에서 보면 다 가변비용이 될 수 있습니다.
그래서 경제학에서의 장기(long-run)란, 고정비용이 없는 정도의 기간을 뜻합니다. 반대로 단기(short-run)는 한 개라도 고정비용이 있는 경우입니다.
수확체감의 법칙과 단기생산함수
기업이 생산을 위해 투입하는 게 크게 봐서 두 가지입니다. 첫째, 자본(재)가 있어야 합니다. 둘째, 노동력이 있어야 합니다. 이 둘을 투입해야 생산이 됩니다. 자본재는 설비나 공장 같이 인위적으로 생산된 생산요소입니다. 자본재는 노동과 달리 고정비용적인 성격이 강합니다. 한 번 지어진 공장을 옮긴다는 것은 노동을 늘리거나 줄이는 것에 비해 훨씬 더 힘듭니다. 자본을 K(capital)라 하고, 노동을 L(labor)이라 하면, 생산량 Q는 다음과 같이 표현할 수 있습니다.
Q = f(L,K)
Q는 노동 L과 자본 K를 투여했을 때 최대로 생산할 수 있는 생산량입니다. 위 식을 생산함수라 합니다. 이 때 함수 f는 생산기술입니다. 철수는 L(노동) 1단위와 K(자본) 1단위를 투입해서 10개를 생산했는데 영희는 똑같은 양의 K와 L을 투입하고 20개를 생산했다면 영희가 갖고 있는 생산기술(f)이 더 효율적인 생산기술입니다. 즉, 더 뛰어난 생산기술은 동일한 L, K를 결합해서 훨씬 더 큰 Q를 기록하게 하는 기술입니다.
그러면 L을 어느 정도 투입하고, 또 K를 어느 정도 투입해야 가장 비용은 적게 들어가면서 최대한의 생산을 해낼 수 있을까요? 문제를 단순화하기 위해 우선 자본은 일정한데 노동 투입량만 변화시키면 생산량 Q가 어떻게 되는지 생각해 봅시다. 현실적으로도 자본재는 고정비용에 가깝기 때문에 일정한 K에서 L의 투입량을 변화시키는 경우가 많습니다.
예컨데 공장에서 사원을 2명을 쓰고 있었는데, 4명을 쓰면 당연히 생산량도 더 커집니다. 분업이 이뤄지고 기타 효율성이 증가합니다. 일단은 L이 늘면 Q도 늘어난다고 생각해 볼 수 있습니다. 그렇지만 공장 규모가 한정되어 있는데 노동을 한없이 늘려 가면 어떻게 될까요? 어느 수준을 넘어가면 노동 L을 늘려도 더 이상 생산 Q가 변하지 않게 됩니다. 또는 공장 규모에 비해 지나치게 많이 투입된 L에 의해 생산 Q가 줄어들 수도 있습니다. 그래서 다음과 같이 그래프를 그릴 수 있습니다.
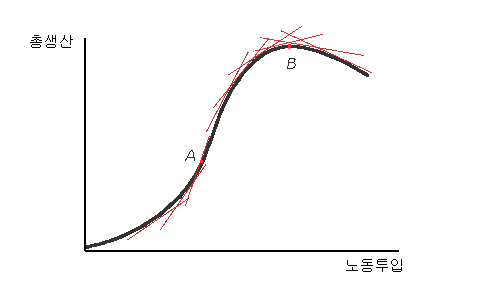
위 그래프를 보면 노동 투입을 늘리면 생산량이 늘기는 하는데 어느 시점부터는 노동 1단위 투입당 생산량 증가분(곡선의 기울기; 빨간 접선의 기울기; 곡선의 미분값)이 점점 줄어든다는 것을 알 수 있습니다. 이렇게 노동 1단위를 더 투입했을 때 늘어나는 생산을 한계생산(marginal production)이라 합니다. 접선의 기울기가 한계생산입니다. 한계생산은 처음 A점까지는 증가하다가 그 이후로는 감소합니다. K가 한정된 상태에서 L 투입을 늘리면 어느 순간부터 생산효율이 더 떨어지는 것입니다. 곡선의 기울기가 증가하다가 변곡점을 지난 뒤 꺾이면서 반대로 줄어듭니다. 아래로 볼록하던 그래프가 변곡점 이후에는 위로 볼록해집니다.
이렇게 가변투입요소를 늘려나가면 처음에는 한계생산이 늘어나다가 어느 시점부터는 줄어드는 것을 "한계생산 체감의 법칙", 또는 "수확체감의 법칙"(Laws of diminishing returns)이라고 합니다. 농사를 지을 때, 일하는 시간을 1시간에서 2시간으로 늘리면 수확량이 몇 배 더 늘어나지만 일하는 시간을 10시간에서 11시간으로 늘리는 경우에는 그 늘어나는 정도(한계생산)가 훨씬 줄어듭니다.
총생산의 경우는 한계생산이 줄어들고 나서도(A 점 이후) 계속 증가합니다. 노동 한 단위 당 생산이 더 늘어나는 정도는 줄지만 생산량 전체는 계속 증가하는 것입니다. 하지만 이 역시 어느 시점에 다다르면 한계생산 감소폭이 매우 커져서 총생산을 줄입니다. 그래프에서 B 점 이후가 그 부분입니다.
평균생산은 한계생산과 달리 생산량의 평균을 의미합니다. 노동 10단위를 투입해서 200이라는 총생산을 얻었다면, 노동 1단위당의 평균생산량은 200/10 = 20입니다.
장기생산함수와 등량곡선
이번에는 L뿐만 아니라 K도 함께 변하는 경우의 총생산에 대해 생각해 봅시다. K도 변한다는 것은 공장, 기계설비 같은 자본재 투입량도 변하는 것이므로 고정비가 없는 장기에서의 생산을 생각하는 것입니다. K와 L이 동시에 변하는 것을 2차원 평면에 그리기 위해서 등량곡선(Isoquant curve)이란 개념을 도입합니다.
등량곡선의 정의는 다음과 같습니다.
등량곡선: 똑같은 상품의 양을 생산할 수 있게 만드는 생산요소의 조합들로 구성된 집합을 그림으로 나타낸 것
총생산 50을 하는데 노동 10과 자본 30을 투입해도 되고 노동 20에 자본 20을 투입해도 된다면, 이렇게 똑같은 총생산을 나타내는 K와 L의 조합을 좌표축상에 다음과 같이 나타낼 수 있습니다.
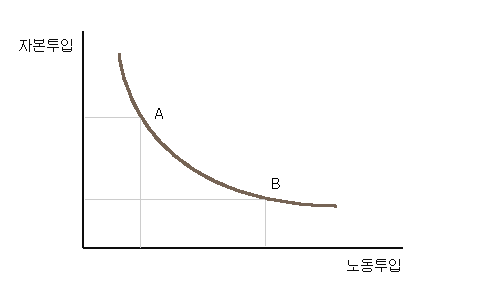
그래프에서 A는 노동을 적게 투입하고 자본을 많이 투입한 경우입니다. B는 노동을 많이 투입하고 자본은 적게 투입한 경우입니다. 어떤 식으로 했든 A점이나 B점이나 총생산은 똑같습니다. 이처럼 총생산이 똑같아지는 여러 점들을 이은 곡선이 바로 등량곡선이며, 등량곡선은 다음과 같은 특징을 갖습니다.
- 등량곡선은 우하향: 어떤 한 요소를 더 많이 투입하면 다른 요소는 조금만 투입해도 똑같은 생산량이 나오기 때문입니다.
- 원점에서 멀리 떨어져 있을 수록 더 많은 생산량: 노동과 자본을 함께 늘리면 그래프는 훨씬 더 바깥에 그려집니다.
- 두 등량곡선은 교차하지 않음: 같은 노동에 같은 자본을 투입했다면 전혀 다른 생산량이 나올 수 없습니다.
- 원점에 대해 볼록: 이것은 밑에서 설명합니다.
등량곡선은 왜 원점에 대해 볼록할까요? 한계기술대체율 체감의 법칙이 작용하기 때문입니다.
그래프에서 오른쪽 부분은 노동 투입량은 많은데 자본 투입량은 매우 적은 곳입니다. 노동 투입이 많기 때문에 그래프의 왼 편에 비해 더 적은 자본 투입만으로도 동일한 생산을 기록하는 것입니다. 한 쪽 자원이 희소해질수록 그 자원을 대체하는 데 다른 자원이 더 많이 필요하다는 의미입니다. 그래프는 우하향하면서 자본이 희소할수록 동일 생산량을 기록하기 위해서는 더 많은 노동 투입이 필요하므로 원점에 대해 볼록해집니다.
한계기술대체율(Marginal rate of technical substitution)은 위와 같이 동일한 총생산을 기록하는 노동과 자본 사이의 비율입니다. 동일한 생산량 Q에서 노동 1단위를 자본으로 표시하면 어느 정도 크기가 되는지 그 비율을 의미합니다. 한계기술대체율의 공식은 이렇습니다.
RTS = MPL/MPK
RTS는 한계기술대체율이고 MPL은 노동의 한계생산, MPK는 자본의 한계생산입니다. 한 쪽을 늘리려면 한 쪽은 줄어들어서 두 개의 부호가 다르므로 마이너스값이 됩니다만, RTS는 서로 대체되는 '비율'을 계산하는 것이므로 노동 투입, 자본 투입의 절대값 비율로 계산합니다.
RTS와 등량곡선의 기울기 사이에는 어떤 관계가 있을까요? 자본 투입을 줄이면서 동일한 생산을 기록하려면 노동 투입을 늘려야 합니다. 노동 투입양을 dL이라 하고 자본 투입양을 dK라 하면 등량곡선상의 모든 점은 dL 투입을 늘리는 것에 따른 생산량의 증가분과 dK 투입을 줄이는 것에 따른 생산량의 감소분이 같아야 합니다. 그래야 동일한 생산량을 기록하기 때문입니다. 따라서,
dL x MPL = -dK x MPK
-(dK/dL) = (MPL/MPK)
즉, 한계기술대체율 RTS는 등량곡선 기울기와 같습니다. 위 그래프를 다시 봅시다. 자본 2단위가 노동 2단위와 대체되는 점에서의 한계기술대체율은 -(dK/dL) = -(-2/2) = 1입니다. 자본 1단위가 노동 3단위와 대체되는 점에서의 한계기술대체율은 -(dK/dL) = -(-1/3) = 1/3입니다. 이렇게 그래프의 오른쪽으로 갈수록 한계기술대체율이 줄어듭니다. 이것을 한계기술대체율 체감의 법칙이라고 합니다.
단기생산함수에서는 한계생산체감의 법칙이 적용됩니다만 장기생산함수에서는 K와 L 둘 다 변하는 것이므로 K와 L의 투입비율은 일정하게 하면서 투입을 늘릴 때 생산이 얼마나 느는지 주는지를 생각합니다. 이것을 규모에 대한 수익(returns to scale; 규모에 대한 수확)이라 합니다. 규모에 대한 수익(수확)이 체증한다는 것은 투입비율은 일정하게 하면서 K와 L이 투입량을 1단위 늘릴 때 총생산이 1단위 이상 늘어나는 것입니다. 규모에 대한 수익이 체감한다는 것은 투입 규모를 1단위 늘릴 때 총생산이 1단위보다 적게 늘어나는 것이고 규모에 대한 수익 불변은 투입을 1단위 늘릴 때 총생산도 1단위가 늘어나는 것입니다. Q = f(L,K)일 때 이것을 식으로 써 보면,
af(L,K) < f(aL, aK): Increasing returns to scale
af(L,K) = f(aL, aK): Constant returns to scale
af(L,K) > f(aL, aK): Diminishing returns to scale
a는 1보다 큰 상수입니다. 전통적인 경제는 대부분 장기적으로 규모에 대한 수익체감 또는 수익불변이 적용되었습니다만 규모에 대한 수익체증이 적용되는 지식상품(knowledge product)이 나타나고 있습니다. 자세한 내용은 수확체증과 새로운 비즈니스의 세계를 참고하세요.
등비용곡선(iso-cost curve)
위에서는 등량곡선을 얘기했었습니다. 동일한 총생산을 기록하는 노동과 자본의 조합입니다. 이번에는 비용을 기준으로 생각해서, 주어진 총지출 한도내에서 사용할 수 있는 노동과 자본의 조합에 대해서 생각해 봅시다.
만약 총 지출할 수 있는 규모가 6천만원인데, 노동은 단위당 20만원, 자본은 단위당 30만원이라고 합시다. 그 경우 6천만원을 모두 노동 구입에만 사용하면 300단위의 노동을 투입할 수 있고, 반대로 모두 자본을 구입하면 자본 200단위를 투입할 수 있습니다. 이렇게 6천만원으로 투입할 수 있는 여러 가지 자본과 노동의 조합을 그래프로 나타내보면 다음과 같이 됩니다.
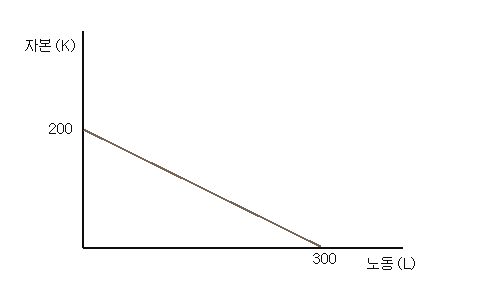
그래프 선상의 모든 점들은 모두 6천만원을 노동 몇 단위, 자본 몇 단위로 조합한 점들입니다. 그러므로 식으로 써보면,
20L + 30K = 6000만
이것을 만족하는 순서쌍 (L,K)가 바로 그래프입니다. 위 식의 Y절편은 K = -2/3L + 200에서 200입니다. Y절편은 L이 0, 즉, 순전히 자본에만 6000만원을 사용할 경우의 자본 투하량이 되고, X절편은 반대로 순전히 노동에만 사용할 경우의 노동의 투하량이 됩니다. 이것을 더 일반화해서, 총비용 C가 있는데, 자본 1단위는 v, 노동 1단위는 w일 때 어떻게 되는지 생각해 봅시다. 식으로 써보면.
wL + vK = C
가 되어서,
이를 K =로 풀면,
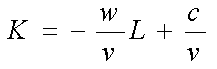
이 됩니다.
이제 기업의 비용극소화 조건을 얘기할 수 있습니다.
기업 비용극소화의 조건
비용극소화란 동일한 양을 생산할 때 비용이 최소화인 조건입니다. 따라서 등량곡선과 만나는 여러 개의 등비용곡선 중에서 가장 비용이 낮는 것을 찾아내면 됩니다. 그래프로 살펴보면,
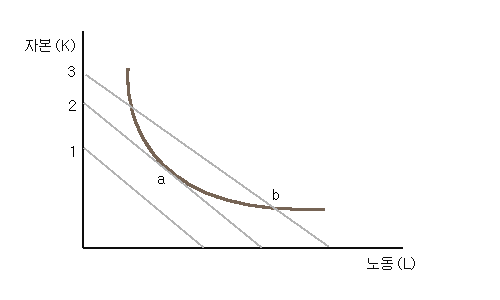
위의 1,2,3은 등비용선인데, 원점에서 먼 것일수록 더 많은 비용을 투입한 것을 나타냅니다.
일단 1번 등비용선은 등량곡선과 만나지 않습니다. 그 얘기는 1번 정도의 자본-노동 투입으로는 그래프상의 등량곡선이 나타내는 만큼의 총생산을 할 수 없다는 의미입니다.
b점의 경우는, 이 점을 지나는 등비용선이 3번입니다. a점의 경우는 2번 등비용선이 등량곡선과 만납니다. 2번보다는 3번 등비용선이 더 많은 비용을 투하하는 것이므로 2번의 경우가 동일한 생산을 할 때 더 비용이 적게 드는 등비용선입니다. 그런데 그래프를 잘 보면, 등량곡선과 등비용선이 접할 때 등비용선이 원점에 가장 가깝다는 것을 알 수 있습니다. (아예 1번처럼 안만나는 것은 볼 필요가 없습니다.)
따라서 비용극소화의 조건은 등량곡선과 등비용선이 접할 때이므로, 등량곡선의 기울기가 등비용선의 기울기와 같아질 때입니다.
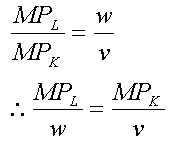
한계기술대체율이 등비용선의 기울기와 같을 때입니다. w는 노동의 1단위의 가격이고, v는 자본 1단위의 가격이라면, "노동 구입에 지출한 1원당의 한계생산이 자본 구입에 지출한 1원당 한계생산과 같다"가 됩니다.
이것이 기업의 비용극소화 조건입니다.
'경영:경제' 카테고리의 다른 글
| [재무관리학] 정보비대칭, 레몬의 문제, 대리인 문제 (0) | 2020.07.02 |
|---|---|
| [조직행동론] 의사결정 이론 (Decision making) (2) | 2020.07.01 |
| [경제학] 소비이론: 무차별곡선과 소비자의 선택 (0) | 2020.07.01 |
| [조직행동론] 커뮤니케이션 이론 (0) | 2020.07.01 |
| 파지티브 피드백 경제 (Positive feedbacks in the economy) (0) | 2020.06.30 |
